LOOK:零知识证明： Plookup算法介绍

最近有空看了看Plookup的论文。针对对电路描述不友好的操作（比如bit操作），Plookup给出了新的思路和证明方式。给定某个操作的真值表示（lookup table），证明某个操作的输入/输出是在真值表中。这种方式，相对之前的bit计算约束方式，降低约束的个数，提高了电路效率。

Plookup的论文下载地址如下：

https://eprint.iacr.org/2020/315.pdf

基本思想

Plookup尝试解决的问题是，给定两个集合，证明某个集合的元素在另外一个集合中。给定两个集合t和f，s是f排序后的结果。如果t中的元素最少在f中出现过一次。判别f中的元素是否包括在t中，只需要比较元素差的集合：

零知识证明技术开发公司StarkWare推出第一个公开版本Cairo 1.0:1月6日消息，零知识证明技术开发公司 StarkWare 宣布推出第一个公开版本的 Cairo 1.0，Cairo 于 2020 年作为图灵完备的编程语言首次推出，用于高效编写 STARK 可证明的程序。Cairo 1.0 中最重要的变化之一是语法，新版本的 Cairo 允许编写更安全的代码。Cairo 1.0 还引入了 Sierra，这是一种新的中间表示，可确保每次 Cairo 运行都可以得到证明。StarkWare 表示，预计在接下来的几周内，提供与旧版本相同的 Cairo 1.0 功能，对 StarkNet 合约的支持将在即将到来的 StarkNet Alpha 版本中加入。[2023/1/6 10:24:18]

零知识证明初创公司RISC Zero完成1200万美元种子轮融资:8月9日消息，零知识证明初创公司 RISC Zero 宣布完成 1200 万美元种子轮融资，Bain Capital Crypto 领投，Geometry 、D1 Ventures 和 Cota Capital 等参投。本轮所融资金将用于构建对开发人员友好的可扩展区块链。今年 3 月，RISC Zero 推出了零知识证明虚拟机，该虚拟机使开发人员能够构建零知识证明，并使用各种编程语言在任何计算机上执行。（The Block）[2022/8/9 12:13:26]

举个例子，t是{1，4，8}的集合，元素的差异集合为{3, 4}，分别是4-1，8-4。如果s只有t中的元素组成，并且每个元素最少出现一次，例如{1，1，4，8，8，8}，元素的差异集合也为{3，4}。如果s中的元素并不完全是t中的元素，那即使在元素差异集合一样的情况下，也不能说明s中元素在t的集合中。例如s为{1，5，5，5，8，8}，元素的差异集合也为{3，4}，分别是8-5，5-1。

以太坊基金会、AMD、Polkadot 发起 700 万美元竞赛以促进零知识扩展:金色财经报道，ZPrize于4月19日宣布，多个加密货币项目联合起来，为使用零知识（ZK）证明的创新团队提供700万美元的奖金。该竞赛由21个Web3组织支持，包括Polygon、Polkadot、Mina和Ethereum基金会。AMD-Xilinx还将为参赛团队提供高功率的计算设备。ZPrize在一份声明中说，参赛团队将尝试设计 \"新的算法和技术，以实现最好的零知识系统无法比拟的性能指标。\"获奖者必须将其提交的材料开源，以便其他开发者能够将任何突破性的东西整合到他们的工作中。[2022/4/20 14:34:54]

论文提出，可以引入一个随机因子，将前后两个元素相加的方法，确定两个集合的依赖关系。

定义多项式

在基本思想的基础上，论文在第三章定义了两个多项式F和G：

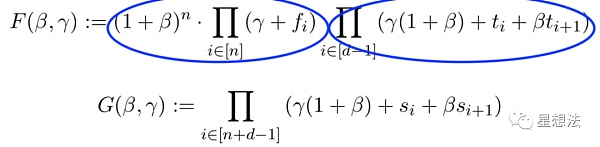
如果F和G相互对等，有且如下的条件成立：

f集合属于t

s是(f，t)的并集，并且按照t中的元素排序

如果条件成立，可以推导出两个多项式相等。F多项式可以看成是两部分组成，分别是两个连乘。后面的连乘可以看成是t中的元素连乘。前面的连乘，可以看成是f中元素的连乘。因为f中的元素属于t，则f中的元素的连乘，可以想象成多个相同元素的连乘。反之，因为beta和gamma的随机因子，也能从F和G对等条件推出满足的两个条件。具体的证明过程，可以查看论文的第三章。

在定义多项式的基础上，问题可以转化成两个多项式相等。

Plookup协议

已知f和t，可以排序得到s。因为s由f和t合并而成，s可以由两个函数h1和h2表示。关键在于第4步，定义了Z函数：

Z(g) = 1 - 初始为1

Z(x) 是两种多项式表示的商

Z(g^(n+1)) = 1 - n+1元素的连乘，两种多项式表达式相等

验证者，除了查看Z函数外，额外还要查看h1/h2连续性。

论文进一步将协议推广到更通用的情况，并给出了t中元素是连续情况下的优化协议。感兴趣的小伙伴可以自行查看。

Plookup提出了一种明确输入/输出的情况下，如何证明某个函数的运算正确的协议。输入输出定义成lookup表，计算的输入/结果只要在该lookup表中即表示运算正确。和Plonk采用同样的思路，Plookup定义了问题的多项式表示，证明了Z函数的递归表示和边界。

标签：LOOKOKUCAIROAIRlooks币投资机构Kazoku INUCairo FinanceCAIRO币

比特币价格实时行情热门资讯