DEFI:零知识证明：身份隐私中的ZK

在区块链世界中，身份可以以多种方式表现出来。真实世界的实体(如人或组织)可以在一个或多个区块链上采用不同的形式，区块链上的一个身份可以代表几个真实世界的实体。这样的身份可以通过拥有私钥、拥有特殊类型的NFT、参与某种类型的 DeFi 等进行建立。

图1：数字身份演示

这种通用且灵活的身份概念可以实现前所未有的用例和体验——但我们也同时需要注意隐私。一个人的身份可能是以一种特定的方式相互关联的多种事物，但只有其中的某一部分可能在一个环境中才是最重要的。例如，一场只允许BAYC NFT持有者参加的音乐会的组织者并不真正关心你拥有哪一个NFT，只要你至少拥有其中一个就可以。参加DeFi会议可能要求去年你在某个DeFi交易所借出了5万个代币，但不确切说明借出了多少、参与了多长时间等。

数据：过去一周零知识区块链上的交易量和投资者存款激增:5月24日消息，DeFi用户正涌向使用“零知识证明”的基于以太坊的区块链，DefiLlama数据显示，zkSync Era、Starknet和Polygon zkEVM的活动在过去一周大幅飙升，这些链上去中心化交易所交易量过去一周分别增长了88%、48%和230%，总锁定价值(Total Value Locked，简称TVL) 过去一周增长分别增长了13%、16%和219%。[2023/5/24 15:22:47]

零知识(ZK)证明可以真正实现这样的用例，同时为相关实体提供数学上可证明的隐私。为了进一步阐述这一点，让我们回到前一段的两个例子。对于第一个例子，ZK证明将表明一个想要参加音乐会的人P知道一个地址A的密钥，该地址属于BAYC NFT持有者的10,000个地址集。进一步分解：

DeGate 发布发展蓝图，将优先实现基于零知识证明技术的以太坊二层订单薄交易协议:据官方消息，以太坊二层交易协议 DeGate 发布最新发展蓝图，对原有的发展路线进行了调整，将优先上线订单薄交易，并最终形成订单薄交易、AMM 交易、保证金交易三者并存的产品架构。

DeGate 表示，随着 Layer2、以太坊 2.0 等技术的落地，区块链使用成本将大幅降低，因此更能满足交易者需求、资金利用率更高的订单薄交易有可能产生更大的市场需求。DeGate 的订单簿交易系统将拥有即时挂单撤单、挂单撤单免手续费、maker 交易免手续费、taker 直接交易等功能或优势。[2021/5/26 22:46:41]

公共输入是在链中某一特定NFT的所有地址的集合S;；

私人输入P为密钥sk1；

西班牙跨国银行BBVA探索零知识证明及加密技术:5月4日消息，总部位于西班牙的跨国银行Bilbao Vizcaya Argentaria银行（BBVA）宣布与马德里研究中心IMDEA Software Institution合作，以探索零知识证明（ZKP）以及其他“先进的加密技术”。（Cointelegraph）[2020/5/5]

我们想在ZK中证明的是，从sk派生的地址在集合S中。

在零知识学术文献中，这种证明通常被称为成员证明。有几种方法可以生成这样的证明。如果集合不是太大，可以使用RSA累加器。

使用RSA累加器，集合S可以用一个短值表示——成员证明也很短。在S中添加或删除地址的代价也很低，与累计值的数量无关。然而，在最坏的情况下，累积集合S和产生证明所花费的时间可能与S的大小成线性关系(实际的时间范围取决于设置的具体情况，甚至可能是恒定时间)。这里还有另一个问题：我们不仅想证明某个地址A在集合中，而且还想证明A是从sk派生出来的。我们可以为前者设计自定义 ZK 协议（例如，离散对数知识) ，但通用的ZK系统通常最适合后者。另一个问题是以一种有效的方式将三个组件粘合在一起(成员关系、离散日志和哈希的原像)。

动态 | 波场社区TRONZ团队已完成零知识证明匿名交易公测:波场社区TRONZ团队已完成零知识证明匿名交易公测，测试网已经顺利部署。匿名交易即将在波场TRON主网上线，现已开启主网MPC流程，社区用户均可参与。Github参考地址可见原文链接。[2019/12/31]

上面提到的第二个用例比第一个要复杂一些。有兴趣参加DeFI会议的人需要表明他们向区块链发送了交易tx(如以太坊)，该区块链在DeFI合约中调用了借贷功能，比如 DF。他们还需要表明，tx转了至少5万个代币，并且它被添加到对应于 2021 年开始和结束的两个区块之间的区块链中。现在，根据区块链，一年内可能会生成数十万区块。每个区块包含的所有交易的哈希(通常称为交易哈希)。ZKP 可以用来表明 tx 被“包含”在某个区块 B 的交易哈希中——而不显示 tx 本身——但这会揭示比预期的还要多的信息。在极端情况下，如果 B 只包含合约 DF 的一笔交易，那么 ZKP 是没有意义的。理想情况下，我们希望证明 tx 包含在2021 年的其中一个区块的交易哈希中。

动态 | 德勤在企业区块链产品中添加零知识证明隐私技术:德勤（Deloitte）周二在阿姆斯特丹举行的ZKProof社区活动上宣布，已在其企业区块链产品中增加了零知识证明隐私技术。德勤与以色列的零知识证明专家QEDIT合作，帮助用户控制区块链共享有关他们所获得的证书和资格的数据。（coindesk）[2019/10/29]

生成一个包含2021年以来所有区块(或至少有一些DF交易的区块)的Merkle树，并证明包含tx的区块只是Merkle树的叶子之一，这将是一个更具可扩展性的方法。对于这个问题：

公共输入是 2021 年以来所有区块集合的Merkle 根(或至少是它们的正确子集)，和合约DF的代码(通过链上的合约地址引用);

私人输入是用于签署 tx的密钥 sk，tx本身，包含tx的区块B，以及B在Merkle树中的路径；

我们想要证明的是：sk 用于签署 tx，tx 包含在 B 中，B 是 Merkle 树的一部分，tx 调用 DF 中的适当函数，并且 tx 转了至少5万个代币（其他tx 的参数应保持隐藏状态）。

我们只是触及了可以在不同用例中进行的大量身份验证的皮毛，ZK语句已经开始显示出一些复杂性。事实上，一旦我们开始更具体地思考，它们会变得更加复杂(诚然，上面关于DeFi会议参与问题的语句相当简单)。其中的复杂性包括：

DF不是直接调用的，而是通过另一个合约或一系列合约进行调用的；

tx包含在区块链中，但对DF的状态没有预期的效果；

会议关心的是以今天的利率借出的实际美元数量，而不是代币。

不过我们不必太担心。ZKP的美妙之处在于，几乎任何你能想到的语句都可以在零知识中被证明(确切地说，任何可以在多项式时间内被验证的关系也可以在零知识中被证明)。虽然 ZKP 的非交互式版本最适合解决 L1 上的机密性、隐私、状态增长、完整性等问题，但交互式证明对于需要基于区块链的身份断言的许多应用程序可能很有意义。

图 2：ZKP 交互式版本示例

上述音乐会入场的例子可以用来说明这一点。对于NFT所有权的ZK成员证明，只需要一个确定的验证者，而不是典型的 L1 设置中的数百或数千个身份不明的验证者。证明者可以主动与验证者接触，并在会话过程中交换多条消息，从而摆脱了非交互式ZK证明固有的复杂性。事实上，证明不必很短，验证者的复杂度也不必很低，因此可以充分探索 ZK-SNARK（最流行的非交互式证明系统，也有简洁的证明）之外的 ZK 证明范围。我们将能够使用具有更好的证明复杂性、底层安全假设等的证明系统。

请参阅下表，了解不同证明系统的高级比较。当我们沿着表格往下看时，证明复杂度和安全性假设变得越来越好，而证明大小变得越来越差。虽然基于mpc的ZK证明系统提供了最好的证明复杂性，并且具备无需信任的设置，但证明是交互式的并且仅适用于特定的验证者（证明者与之交互的那个），所以当身份断言必须对链下的特定一方做出判断时，这可能就不是问题。(ZK证明系统的其他一些特征，如后量子安全性，在表中没有体现。)

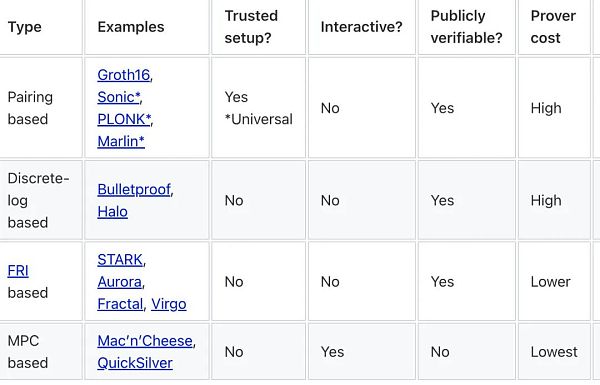
表 1：不同证明系统的高级比较

总之，世界上的身份不一定是基于区块链的，也不一定是基于非区块链的。展望未来，它们当然可以是两者的结合——这将使保护隐私的身份断言变得更加有趣!

Source：https://medium.com/delendum/zk-in-identity-980493401d80

标签：区块链DEFDEFIEFI泰达币区块链交易查询DefyDefikingdefi币归零GEFI

USDC热门资讯