RON:Ronin 黑客计中计 听说过扭曲攻击漏洞吗？

By: Johan

据慢雾安全团队情报，2023 年 3 月 13 日，Ethereum 链上的借贷项目 Euler Finance 遭到攻击，攻击者获利约 2 亿美元。

黑客在攻击完 Euler 后，为了混淆视听逃避追查，转了 100 ETH 给盗取了 Ronin 6.25 亿多美金的黑客拉撒路。拉撒路顺水推舟将计就计，随即给 Euler 黑客发了一条链上加密消息，并回礼了 2 枚 ETH：

消息内容是提示 Euler Exploiter 用 eth-ecies 解密这条消息。

按道理说在公开的环境下，如果 Ronin Exploiter 只是想加密通讯，使?公钥加密是最简单的?案。

    公钥加密：

C = {rG, M + rQ} = {C1, C2}

    私钥解密：

M = M + r(dG) ? d(rG) = C2 ? d(C1)

其中密? C，公钥 Q，私钥 d，随机数 r，消息 M。协议很简单，加密过程不需要?到的私钥，不存在私钥泄露的路径。

使? eth-ecies 加密是因为?便还是另有所图？随后很快就有?指出 eth-ecies 存在安全漏洞，Ronin Exploiter 是想窃取 Euler Exploiter 的私钥。

孙宇晨：正与FTX一起制定解决方案以支持FTX上Tron系Token:11月10日消息，孙宇晨在其社交平台表示，正与FTX一起制定解决方案以支持FTX上Tron系Token（TRX、BTT、JST、SUN、HT），其团队正在积极工作以避免情况恶化，目前情况可控。

此前报道，11月9日，Huobi官方公告，Huobi、波场DAO宣布将永久1：1刚性承兑所有FTX平台内波场系Token（TRX、BTT、JST、SUN、HT），用户需填写表单并登记Huobi账户，Huobi将以此作为根据，与FTX平台协调对账关于TRX、BTT、JST、SUN、HT的提现事宜。[2022/11/10 12:42:33]

是否真的如此？且让我们先分析?下 eth-ecies 存在的是怎么样的?个漏洞。

经过分析，我们发现 eth-ecies 使?了 "elliptic": "^6.4.0"，这是个 Javascript 椭圆曲线库，这个版本的库存在多个安全漏洞，其中?个就是扭曲曲线攻击漏洞(twist attacks)，这个漏洞的成因是在计算 ECDH 共享密钥时没有验证对?的公钥是否在曲线上，攻击者可通过构造??群曲线上的公钥，诱导受害者计算共享密钥，从?破解出受害者私钥。

但是这个漏洞的利?难度是很?的，需要有?常契合的场景才能发起攻击，Ronin Exploiter 是否有机会发起扭曲攻击呢？

ECDH 算法是基于椭圆曲线加密的密钥交换算法。它与传统的 Diffie-Hellman (DH) 算法类似，但是使?的是椭圆曲线上的数学运算来实现密钥交换，从?提供更?的安全性。

链外DeFi聚合层Frontier与以太坊推送服务（EPNS）达成战略合作:链外DeFi聚合层Frontier宣布与以太坊推送服务（EPNS）达成战略合作，以支持去中心化通知服务。该合作关系将允许Frontier以平台无关的方式（移动端、网络、钱包等）向用户发送通知。

双方试点项目和合作主要包括：探索Frontier App中的协议使用；实施和消除任何必要的功能，以实现平稳集成；关于构建SDK的技术讨论，该SDK可作为即插即用解决方案部署到所有加密钱包中；未来可能与Frontier钱包整合。[2021/4/29 21:10:05]

下?是 ECDH 算法的步骤：

1. ?成椭圆曲线：在密钥交换之前，通信双?需要选择?个椭圆曲线，该曲线必须满??些数学特性，例如离散对数问题。

2. ?成私钥和公钥：每个通信?都需要?成?对私钥和公钥。私钥是?个随机数，?于计算公钥。公钥是?个点，它在椭圆曲线上，并由私钥计算得出。

3. 交换公钥：通信双?将??的公钥发送给对?。

4. 计算共享密钥：通信双?使?对?发送的公钥和??的私钥计算出?个共享密钥。这个共享密钥可以?于加密通信中的数据，保证通信的机密性。

为了?便描述下? Alice 和 Bob 分别代表上?双?，G 为基点，假设：

Alice 的私钥是 a，则 Alice 公钥是 A = aG；

Bob 的私钥中 b，则 Bob 公钥是 B = bG。

核?知识点在共享密钥计算?法，根据群的乘法交换律，他们只要获取到对?的公钥就可以计算出共享密钥：

波场TRON账户总数突破2400万:3月8日，根据TRONSCAN波场区块链浏览器（https://tronscan.io）最新数据显示，波场TRON账户总数达到24,190,786，突破2400万。波场TRON各项数据稳中前进，波场生态逐渐强大的同时，也将迎来更多交易量。[2021/3/8 18:24:15]

                                               S = aB = a(bG) = b(aG) = bA

如果 Alice 想要刺探 Bob 的私钥，她可以选择?个阶数 q ?常?（点的数量?常少）的曲线点 H（这个点不是对应任何特定私钥的公钥，但是 Bob 并不知道），由于群是循环群，Bob 在计算 S′  = bH 时，他得到的 S′  将在这些少量点群以内。Alice 不知道 Bob 的私钥 b，但可以通过穷举得到满? S′ = xH 的 x，此时 b ≡ x  mod q 。显然 x 很?，最?为 q。

Electroneum成为欧洲区块链组织第十名成员:金色财经报道，加密支付网络Electroneum（ETN）已成为欧洲区块链（Blockchain for Europe）第十名成员。该组织还包括Ripple和Cardano等其他成员，致力于区块链推广和教育，帮助欧盟保持在全球创新前沿。[2020/10/10]

需要多少个扭曲点呢？这取决于每?次选择的阶数 q，需要阶数相乘能超过私钥的最?值，即满?：

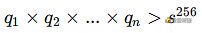
如果我每次选择的 q ??点，那么需要交互的次数 n 就可以少?点，但 q 越?意味着穷举的难度越?，所以这?需要根据 Alice 的运算性能做?个取舍。

上?我们分析了 ECDH 算法的?险和攻击原理，我们再回来看 eth-ecies 这个库，实际上它使?的只是?个类似 ECDH 的算法，它在构造共享私钥时使?的是临时密钥，根本不需要?到加密?的私钥，所以并不会对加密?构成?险。

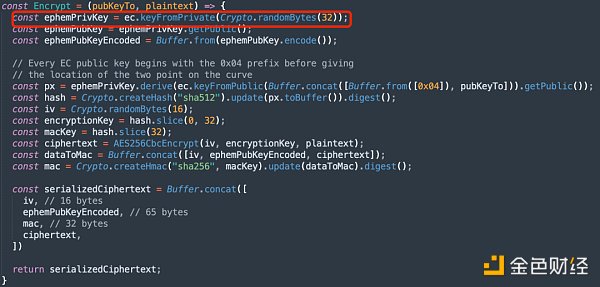
那么有没有可能 Ronin Exploiter 是想利?社会?程学引导 Euler Exploiter 使?其它有问题的?具呢？?如我们熟知的 PGP 加密协议？

巧的很，我们很快就发现被?泛使?的开源库 openpgpjs 最新版本 v5.7.0 还在使?了低版本的 "/img/2023525204111/5.jpg" />

故事结束了，我觉得 Ronin Exploiter 使?低版本 elliptic 存在的漏洞去隐秘的窃取 Euler Exploiter 私钥的可能性不?，?于那条链上消息，可能真的是为了共商?计，更进?步的图谋不轨需要更加?超的社会?程学?段了，但 Euler Exploiter 已经警觉。

上?提到了扭曲攻击的原理，实际?程实现上仍然有?个问题需要解决：

1. 如何构造扭曲的点？

2. 当 Bob ?共享密钥 S' 加密消息时，它并不会把 S' 传输给 Alice，因为根据协议 Bob 认为 Alice 是已经知道这个密钥的，那么 Alice 如何获取 S' 呢？

这?以 Curve25519 曲线为例，它的曲线?程是：

我们随意改变其中的?个参数，得到?条新的曲线，?如：

使? sagemath 数学软件来表示：

p = 2**255-19 E = EllipticCurve(GF(p), [0,48666,0,1,0])然后我们计算它的阶数，并对这个阶数进?因式分解：

Grp = E.abelian_group() G = Grp.gens() Gorder = G.order() print( "{0} = {1}".format(Gorder, factor(Gorder)) )计算结果：

...= 2 * 3049 * 14821 * 19442993 * 32947377140686418620740736789682514948650410565397852612808537选择 19442993 这个??适中的数，?中国剩余定理创建?个含有 19442993 个元素的?群： 

x = crt([1,0], [19442993, Gorder//19442993]) P1 = x * G到这?我们就得到了第?个扭曲的点，把它当作公钥发送给 Bob，Bob 就可以计算第?个共享密钥：

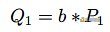
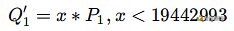
最终得到的结果可表示为：

使?中国剩余定理即可计算出私钥 b：

x = crt([ x1, x2, x3, x4, x5, x6, x7, x8, x9], [ 19442993, 3645143, 184879577, 5110460161, 15272631587, 208137522259, 64927105657, 60824497, 213156431]) print(x == b) print(hex(x))总结本?我们通过?个不同常理的对话开始研究了椭圆曲线加密算法中的扭曲曲线攻击，分析了漏洞的存在的原因，虽然漏洞利?场景有限，但不失为?个很有价值的漏洞，希望能对?家的学习研究有所启发。

最后，感谢领先的?站式数字资产?托管服务商 Safeheron 提供的专业技术建议。

参考资料：

.https://etherscan.io/tx/0xcf0b3487dc443f1ef92b4fe27ff7f89e07588cdc0e2b37d50adb8158c697cea6

. https://github.com/LimelabsTech/eth-ecies

. GitHub - openpgpjs/openpgpjs: OpenPGP implementation for JavaScript

. Elliptic curve constructor - Elliptic curves

慢雾科技

个人专栏

阅读更多

金色财经 善欧巴

金色早8点

白话区块链

欧科云链

Odaily星球日报

Arcane Labs

MarsBit

深潮TechFlow

BTCStudy

链得得

标签：NBSBSPRONETHnbs币官网BSPAY价格Final Frontierethnical

币安app官网下载热门资讯