数字货币:数字签名：基于椭圆曲线的签名方案

在数字时代中，数字化文档的认证性、完整性和不可否认性，是实现信息化安全的基本要求。数字签名则是满足上述要求的主要方式之一，亦是现代密码学的研究内容之一。

数字签名有哪些形式？基于密码学的数字签名优势几何？有哪些常用的数字签名实现方案？使用过程中又潜藏何等风险？我们将先从理解概念为始，再为大家逐步深入介绍。

区块链百科No.34：基于椭圆曲线签名方案

随着计算机信息处理能力的不断提高，对密钥长度的要求也越来越高，这个问题对于存储能力受限的系统来说显得尤为突出。

椭圆曲线密码体制（ECC）的提出改变了这种状况，它可以用更短的密钥提供与其他体制相当的或者更高级的安全，并已成为迄今被实践证明安全、有效、应用较广的3种公钥密码体制之一。本文将继续为大家介绍基于椭圆曲线的数字签名方案。

美联储戴利：在平衡数字货币风险方面仍有相当多的工作要做:2月1日消息，美联储戴利：在平衡数字货币风险方面仍有相当多的工作要做。（金十）[2022/2/1 9:25:05]

椭圆曲线在代数学和几何学上，已被广范研究了150年之久，有坚实的理论基础。

所谓椭圆曲线是指维尔斯特斯拉（Weierstrass）方程：

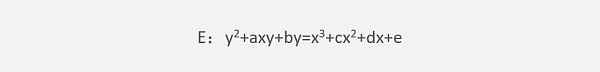
所确定的平面曲线，其中a、b、c、d、e属于域F，其可以是有理数域Q、复数域C，还可以是有限域GF（p）。

椭圆曲线是其上所有点（x、y）的集合，外加一个无穷远点O（定义椭圆曲线上一个特殊的点，记为O，它为仿射平面无穷远的点，称为无穷远点。在xOy平面上，可以看做平行于y轴的所有直线的集合的一种抽象）。

安托将使用IBM Cloud保护数字钱包安全:3月3日，安托（Onchain Custodian）宣布将在其发布的新版SAFE平台上使用IBM Cloud Hyper Protect Crypto Services来提升其基础钱包管理的冷存储功能，通过利用公有云中提供的FIPS 140-2 Level 4认证硬件构建的安全模块（HSM）来实现密钥的生成和存储，具有高度的防篡改功能。

IBM Z（IBM Z as a Service）总监Rohit Badlaney表示：“通过利用IBM云超级保护服务，安托可以构建一个高度灵活且安全的基于云的解决方案，支持像安托这样的托管平台是IBM Cloud Hyper Protect Services非常理想的应用案例。”

安托董事会主席、Onchain CEO达鸿飞表示：“我们一直在与我们精选的合作伙伴一起不断扩大客户群和开放式金融服务产品。随着我们增强的托管解决方案的上线，安托已准备好进一步扩展。我们正在寻找战略投资者来加速我们的扩展。”

安托是一家位于新加坡的数字资产托管平台，于2018年获得复星、DHVC、红杉资本的投资。[2020/3/4]

密码学中普遍采用的是有限域上的椭圆曲线，它是指椭圆曲线方程定义式中，所有的系数都是在某一有限域GF（p）中的元素。它最简单的公式为：

动态 | 2019年浙江十大社科学术热点发布 包括“区块链、人工智能与数字经济研究”:浙江省社科发展研究和评价中心戴道昆发表文章《2019年浙江十大社科学术热点》，其中包括“区块链、人工智能与数字经济研究”。文章指出，全省社科界深入研究区块链等新一轮科技革命和产业变革，为打造数字经济“一号工程”提供智力支持。举办了“人工智能与社会趋势”“认知科学与思维发展”等跨学科系列主题研讨会。推出浙江省社科学者“数字经济引领高质量发展”研究专版；举行第三届中国经济学家高端论坛、“2019浙商（秋季）论坛暨新制造新发展峰会”等会议。（浙江日报）[2020/1/22]

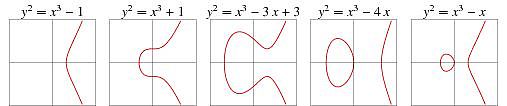
该椭圆曲线上只有有限个离散点，设为N，则N称为椭圆曲线的阶为N。N越大，安全性越高。基于此，椭圆曲线的图示可以表示如下：

金色晨讯 | 中国拘留数字货币盗窃者 华尔街对加密货币需求仍在增加:1.南非税务局宣布常规税收规则适用于数币相关交易。

2.中国拘留三名涉嫌数字货币盗窃嫌疑人。

3.火币矿池通证HPT上线，其中20%将空投给HT用户。

4.蚂蚁金服区块链业务专家称区块链票据可杜绝重复报销。

5.以太猫创始人表示，区块链在亚洲还有很大发展空间。

6.V神提出可将目前交易中使用的最高收费拍卖模式改为固定收费模式。

7.卡巴斯基称，第二季度犯罪分子以ICO名义窃取投资者信息获利230万美元。

8.John McAfee表示最近引发的BitFi钱包争议只是营销手段。

9.华尔街分析师表示，尽管价格下跌但华尔街对加密货币的需求在增加。[2018/8/20]

动态 | 太空望远镜科学研究所用数字货币加速深空研究:区块链公司AIKON今天宣布推出新的数字货币CPU，以及第一个使用它们的客户：太空望远镜科学研究所（STScI）。该研究所的研究人员正使用CPU代币向AIKON合作伙伴HADRON支付费用，以便HADRON的工作人员对哈勃大型存储库的深空图像进行分类。[2018/7/20]

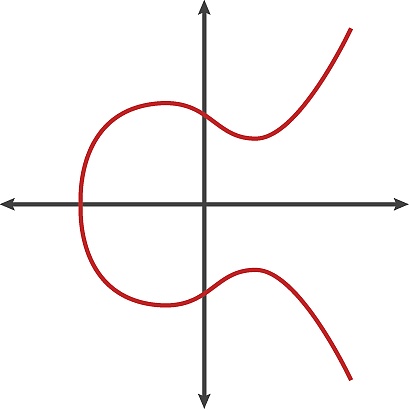
当然，基于不同变量值，椭圆曲线还有其他的表示形式：

当我们仔细观察这些曲线时，能发现一些有趣特性：（1）对称性，即曲线上的任何一点都可以在x轴上反射，并保持曲线不变；（2）任何非垂直直线与曲线的交点至多有三个。

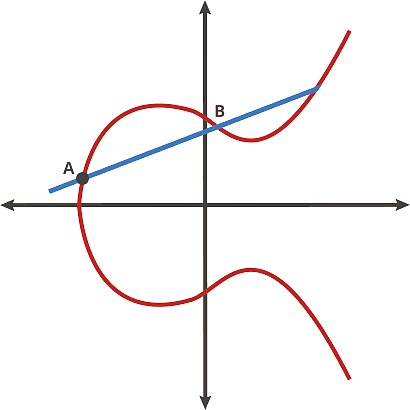
我们可以把这条曲线想象成一场桌球游戏。在曲线上取任意两点并通过它们画一条直线，它将与曲线相交于另一个位置。在这个桌球游戏中，你在A点拿一个球，把它射向B点，当它击中曲线时，球要么直接向上反弹(如果它在x轴以下)，要么直接向下反弹(如果它在x轴以上)到曲线的另一边。我们可以把球看做在两个点间移动，曲线上的任意两点碰撞可得到一个新的点。

A·B = C

或者可以用某一个点自身不断碰撞出新的点。

A·A = B

A·C = D

……

在这个过程中，一个初始点经由n次运算会得到最后到达的点，当你只知道这两个点的值，要找出n是很难的。

这就像一个人在房间里随机玩一段时间桌球游戏，对他而言，按照上面描述的规则一遍又一遍地击球是很容易的。但如果有人走进房间，球刚好结束到达一个点，即使他知道所有的游戏规则，以及球从哪个点开始，也不能确定球到达此处所被击中的次数。容易正向计算，难以反向计算，这也是陷门函数的基础。

1985年，Koblitz和Miller将椭圆曲线引入密码学，提出了基于有限域GF（p）的椭圆曲线上的点集构成群，在这个群上定义离散对数难题并构造出基于其的一类公钥密码体制，即基于椭圆曲线的离散密码体制，其安全性基于椭圆曲线上离散对数问题的难解性。

我们以基于椭圆曲线的ECDSA数字签名实现方案为例，阐述其具体的实现过程。

密钥生成算法

假设GF（p）为有限域，E是有限域GF（p）上的椭圆曲线。选择E上一点G∈E，G的阶为满足安全要求的素数n，即nG=O（O为无穷远点）。

选择一个随机数d，d∈[1，n-1]，计算Q，使得Q=dG。那么公钥为（n，Q），私钥为d。

签名算法

假设待签名的消息为m，经过如下计算过程，签名者对消息m的数字签名为（r，s）。

验证算法

签名接收者B对消息m签名（r，s）的验证过程如下：

判断r和r1的关系，如果相等，则签名有效；否则，签名无效。

除了上述介绍ECDSA方案之外，基于椭圆的数字签名方案还有很多，而类似DSA的其他方案例如Schnorr、EIGamal等方案也都被移植到椭圆曲线有限群上。

从上述介绍可知，数字签名的安全性依赖于基于椭圆曲线的有限群上的离散对数难题。

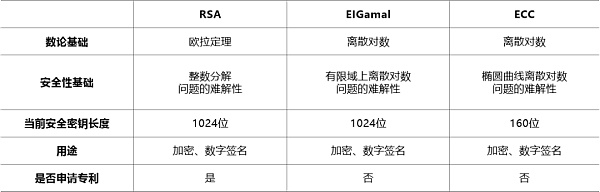
与前章所述RSA数字签名和基于有限域离散对数的数字签名相比，基于椭圆曲线的数字签名方案具有如下特点：在相同的安全强度条件下，签名长度短，密钥存储空间小，适用于存储空间有限，带宽受限、要求高速实现的场合。

此外，椭圆曲线资源丰富，同一有限域上存在着大量不同的椭圆曲线，这也为安全性增加了额外的保障。

正是由于椭圆曲线具有丰富的群结构和多选择性，并可以在保持和RSA、EIGamal体制同样安全性的前提下大大缩短密钥长度，因而有着更为广阔的应用场景。

标签：区块链数字货币OUDCLO有人靠区块链4天就挣了30万央行数字货币是稳定币吗Cloud9BSCCloudbric

币安app下载热门资讯