PLO:学习笔记 | 零知识证明算法之PLONK——协议

上一篇主要描述了PLONK协议里的一个核心部分，用置换校验的方法去证明电路门之间的一致性；接下来，将继续分享如何证明门的约束关系得成立，以及整体的协议剖析。

门约束

举个简单的例子，假如存在一个电路，电路中仅有3个乘法门，对应的约束如下：

L1*R1-O1=0

L2*R2-O2=0

L3*R3-O3=0

进行多项式压缩：定义多项式函数L(X),R(X),O(X)满足：

L(1)=L1,R(1)=R1,O(1)=O1

L(2)=L2,R(2)=R2,O(2)=O2

L(3)=L3,R(3)=R3,O(3)=O3

此时，定义新的多项式函数F(X)，令F(X)=L(X)*R(X)-O(X)

则有：

F(1)=L(1)*R(1)-O(1)=0

F(2)=L(2)*R(2)-O(2)=0

F(3)=L(3)*R(3)-O(3)=0

也就是表明：如果多项式函数F(X)在X=1,2,3处有零点，则说明门关系约束成立。

多项式函数F(X)在X=1,2,3处有零点则表明多项式F(X)可以被(X-1)(X-2)(X-3)整除，为了和论文一致，我们把这个多项式函数设置成Z(X)，即：

F(X)=T(X)*Z(X)==>T(X)=F(X)/Z(X)

孙宇晨：波场4.0标志着波场从学习者到创新者的转变:据最新消息显示，波场TRON创始人兼BitTorrent CEO孙宇晨正在直播中表示：“波场是行业中第一个研发出跨链协议并主网上线的区块链，TICP是一个跨链协议，波场也是业内第一个允许万链互连的区块链。波场确实是业内的头一名真正推出了这样一个万链互联的协议，到今天开发者就可以在波场上实现这些功能。波场4.0之后进入了一个全新的发展阶段，波场4.0标志着从学习者到创新者的转变，具有里程碑意义。波场4.0标志着波场从细分领域的领先到全方位反超再到成为行业的创新领跑者。未来的波场既是操作系统，也是人类未来的金融基础设施。”[2020/7/9]

如果能证明T(X)是一个多项式，则说明多项式F(X)与Z(X)有相同的零点，进而说明门约束关系成立。

一般过程应该如下：

1.P计算F(X)并把F(X)发送给V；

2.V根据Z(X)直接校验F(X)/Z(X)

但是如此过程存在两个问题，一个是复杂性问题，假如F(X)的阶为n，那通信复杂度就是O(n)；而是安全性问题，多项式F(X)完全暴露给V。

那应该如何解决这两个问题呢？最佳的答案可能就是：多项式承诺

多项式承诺

什么是多项式承诺？就是证明方P用一个很短的数据来代表一个多项式F，这些很短的数据可以被验证方V用来验证多项式F在某一点的值确实为证明方P声称的值z。

具体看一下论文里的定义：

学习时报：利用区块链信息传播机制应对舆情提高政府公信力:学习时报发表《以区块链技术应对重大风险事件》文章，文章表示，当前，防控疫情态势持续向好，但是疫情防控过程中也暴露出一些问题，集中体现在决策信息汲取、归集机制不完善。对于基层政府而言，反应时间较长，缺乏及时、准确、可溯源验证的信息发布途径；信息交流不畅，治理工具结构性缺乏等。针对本次疫情中的问题，区块链技术基于其去中心化、不可篡改、可追溯等特性，将区块链技术作为疫情管理系统中的底层技术核心架构，对于提升信息的公开透明度、提升政府公信力、高效分配社会资源等领域具有很大帮助。利用区块链信息传播机制应对舆情提高政府公信力。（学习时报）[2020/3/20]

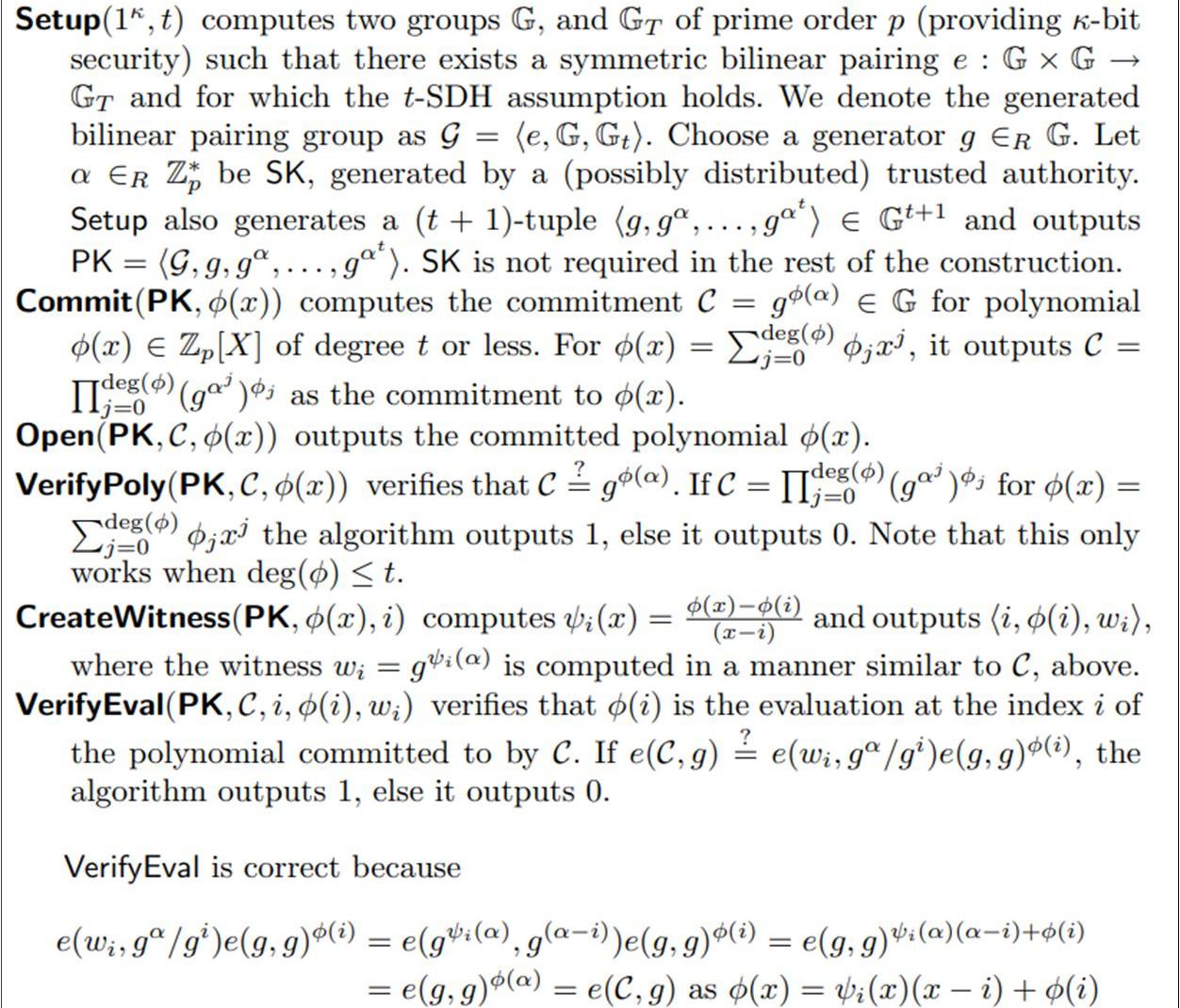
由图可知：

1.Setup:初始化，生成计算多项式承诺需要的一些必备参数；

2.Commit:计算多项式承诺，其结果是一个值；

3.Open:返回与多项式承诺对应的多项式函数；

4.VerifyPoly:验证多项式承诺是否和多项式函数一致；

5.CreateWitness:证明多项式函数在某一点的值是否是证明方P声称的值，具体的数学方法就是：判断多项式是否能被整除，即：

动态 | OKEx学院正式上线 打造一站式区块链学习平台:据OKEx官方消息，OKEx学院正式上线，OKEx学院是OKEx全新打造的区块链&数字资产一站式学习平台，目标是为区块链和数字资产用户提供一站式学习资源，为不同学习阶段的用户提供了系统化学习的窗口。

据了解，目前OKEx学院的学习内容包括新手教程、交易策略、行业研究、区块链词典，以及各类主流币种信息，欢迎登录OKEx官网学习体验。[2020/1/19]

6.VerifyEval:验证方V验证多项式函数在某一点的值是否是证明方P声称的值，具体的数学方法是：利用双线性配对验证其数学乘法逻辑关系。

继续回到我们上面的问题：

证明方如何证明：T(X)=F(X)/Z(X)，我们再简化一下场景，就令Z(X)=X-1，则:

T(X)=F(X)/(X-1)==>T(X)*(X-1)=F(X)==>T(X)*X=F(X)+T(X)

对应多项式承诺的协议可知：证明方P其实是想证明多项式函数F(X)再X=1处的值为0，因此根据协验证方只需要证明：

e(Commit(T(x)),x*G)=？e(Commit(F(x))+Commit(T(x)),G)(双线性配对的性质)

可以看出，利用多项式承诺的数学工具，既可以实现复杂度的优化，又可以实现隐私保护。

协议

接下来分析一下完整的PLONK协议：

Relation

动态 | 衡水市委理论学习中心组（扩大）召开区块链专题学习会:11月28日上午，衡水市委理论学习中心组（扩大）召开区块链专题学习会，深入学习总书记在中央局第十八次集体学习时的重要讲话精神和区块链相关知识。市委常委、秘书长孙世岩孙世岩在主持会议时强调，各级各部门要坚持站位，深入学习领会习总书记重要讲话精神，切实把思想统一到党中央决策部署上来，主动加强对区块链技术的学习研究，熟悉基础知识，掌握相关政策，找准切入点、选好攻坚点，力争在区块链发展大格局中找准衡水位置。要不断加强对新经济、新科技、新模式、新业态的学习，坚持“走出去”与“请进来”相结合，提高开放意识、增强工作本领，为实现换道超车、跨越发展找到更多创新路径。要坚持厚植土壤，深刻认识区块链的变革性作用，探索培养引进一批懂理论、懂技术、懂应用、懂产品的专业人才和复合型人才，推动区块链技术在城市公共服务、医疗服务、企业服务及网络安全等领域发挥作用。（衡水新闻网）[2019/11/29]

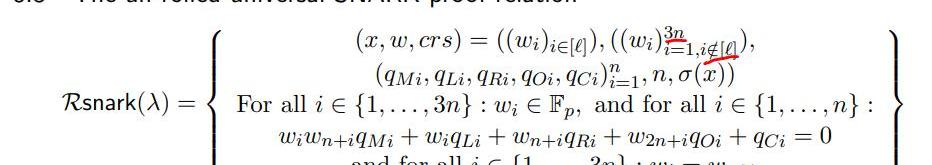
上图表示了PLONK算法里，要证明的一种关系，需要说明的是：

1.w代表着电路里的输入、输出，总共3n个，n是电路里乘法门的数量，每个门都有左输入，右输入和输出，因此w总共有3n个；

声音 | 学习时报：推进数字货币发展必须在安全、可控、可管的前提下稳妥稳步推进:今日，《学习时报》发表题为“积极谋划我国数字货币发展”的分析文章。文章中表示，加强对数字货币研究，谋划我国数字货币发展未来，已经迫在眉睫。针对我国数字货币发展的对策，文章中建议：1.支持移动支付企业国际化发展；2.加快建立我国数字货币发展体系；3.加快制定数字货币监管制度；4.构建数字货币监管技术体系。文章最后还表示，数字经济时代到来，经济社会各个领域都在加快数字化转型，金融领域也不例外，数字货币作为货币数字化发展的重要方向，未来发展势不可挡。然而，货币的数字化和其他领域的数字化具有很大不同，货币具有较强的金融属性，与各国经济、金融、财政、税收、安全等各类政策高度息息相关，发展措施稍不谨慎甚至会引发经济社会破坏性震荡。因此，推进数字货币发展不允许试错，必须在安全、可控、可管的前提下稳妥稳步推进。[2019/8/16]

2.q*代表着选择向量，它的取值对应这这个是乘法门，还是加法门等类似的约束类型

3.σ代表着置换多项式，其表示门之间的一致性约束索引

4.倒数第一个公式代表门之间的约束成立

5.倒数第二个公式代表门的约束关系成立

CRS&P_Input&V_Input

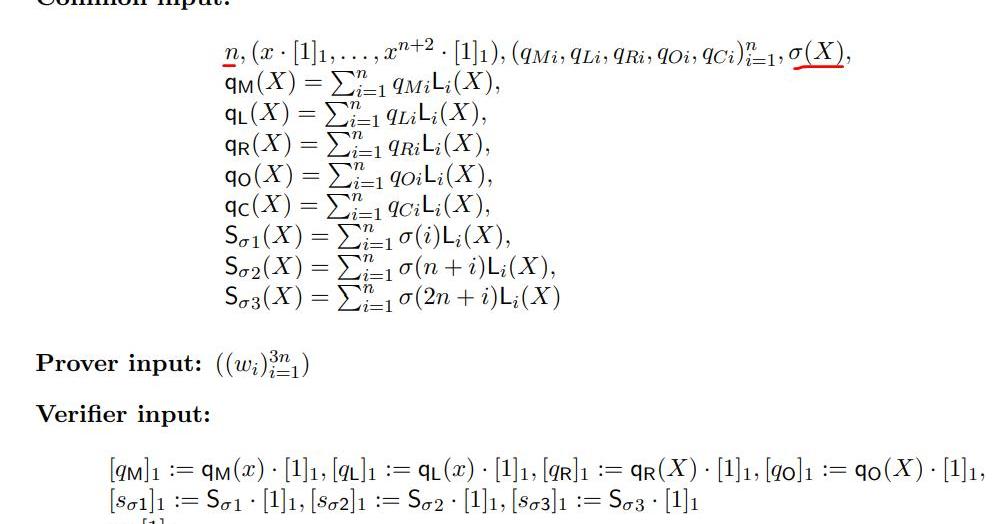
上图表示了PLONK算法里的CRS设置，以及证明方P和验证方V的一些输入，需要说明的是：

1.整个协议都是基于多项式的，因此需要构建对应的多项式形式。

2.多项式σ的阶是3n的，由于和多项式承诺相关的CRS最高的阶位n+2，因此需要把σ拆分成3个多项式S,分别记录每个多项式的置换关系(L,R,O);

3.为了减少通信复杂度和保护隐私，协议基于多项式承诺构建，因此验证方V的输入都是承诺值。

Prove

上图表示了PLONK算法里证明方的一些操作，需要说明的是：

1.b1,...b9是随机数，从用法看是为了安全，但是我暂时也没明白，不加这个随机数，又会有什么安全问题？

2.a(X),b(X),c(X)分别是代表了电路里的左输入，右输入和输出

3.,,表示多项式的承诺值，参考多项式承诺小节里的承诺计算方法

上图表示了PLONK算法里证明方的一些操作，主要是置换校验，参考第一篇的置换校验的协议过程，生成多项式z(X)，需要说明的是：

1.β和?都是用来生成置换校验函数的参数，详见第一篇里f`(x)和g`(x)的生成过程；

2.z(X)的生成方式对应置换校验里跨多项式的生成过程，Li(X)为拉格朗日多项式基，性质满足，尽在x=i的时候为1，其他为0；

3.注意区分ω和w，ω是群H的生成元，是多项式的自变量的取值。w是电路的左输入，右输入和输出，是多项式L,R,O在在群H上的取值。

上图表示了PLONK算法里证明方P的一些操作，主要是把门约束和门之间的一致性约束组合到一起，通过α，需要说明的是：

1.根据前面的描述，门约束多项式和一致性约束多项式在群H上的所有元素都是取值为0的，因此都会被多项式ZH(X)整除，等同于上面所述的T(X);

2.因此，证明方只要能证明整除的结果的确是多项式，那就能证明，门约束多项式和一致性多项式在群H所有元素上取值为0，即所有约束关系成立，即电路逻辑成立；

3.可以知道的是t(X)的阶最高为3n，但是用于计算承诺的CRS只到了n的级别，因此需要把多项式t(X)拆分，然后单独计算承诺值。

上图表示了PLONK算法了证明方P的一些操作，主要根据多项式承诺的协议，前面P算出了多个多项式在点x=z处的值是多少，现在要用多项式承诺协议去证明，这些计算是正确的，需要说明的是：

1.为了减少验证方V的操作复杂度，t(X)的分子部分r(X)在x=z处的值，P计算好，然后验证方直接验证，其他的操作类似；

2.v的值看起来是为了更安全；

3.Wz(X)对应多项式协议里的CreateWitness操作，证明这些多项式r(X),a(X),b(X)等在x=z处的值确实等于r,a,b等，对Wzw(X)同理，并返回承诺值。

Verify

至此，证明方P的所有操作都完事了，接下来都是验证方V的操作。

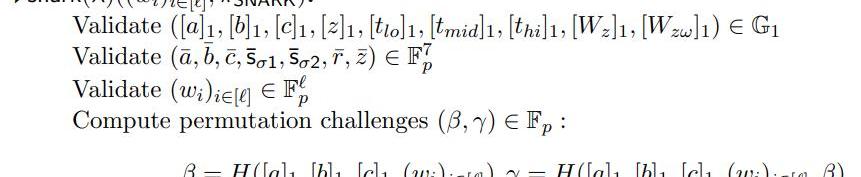
上图表示了PLONK算法里验证方V的一些操作，主要重新生成相关的参数，确保证明方P没有作恶。需要说明的是：

1.从输入看，比较清晰，就是一些公开的输入和证明方P的证明输出；

2.根据输入，生成置换校验过程中需要的一些参数

上图表示了PLONK算法里验证方V的一些操作，对于一些公开的，并且计算复杂度很小的多项式，其在x=z处的值还是需要自己计算，更为方便。需要说明的是：

1.根据证明方P的过程来看，验证方V的核心工作就是验证两个多项式承诺；

2.两个多项式承诺验证需要两个配对，可以通过一个参数组合成一个配对，即μ；

3.在验证前，先计算Wz(x),Wzw(x)的分母在x=z处的值，两部分，减数和被减数，分别对应,。μ作为系数的，就是对应Wzw(X)多项式的。

4.最后通过一个双线性配对操作完成两个多项式承诺的验证。

结束

至此，PLONK算法的协议原理已全部分享完成，公式很密集，但是细分下来，又很有层次感。能坚持看完，已实属不易。各位读者有什么不同的简介，还请指教，谢谢。

标签：区块链PLOLON数字货币区块链通俗易懂的说法Society of Galactic ExplorationELONGD数字货币交易所开发安全解决方案

Luna热门资讯