区块链:学习笔记 | 零知识证明算法之PLONK——电路

最近研究了下零知识证明算法-PLONK。肚子里的墨水又增加了，记一下学习成果与新的体会，和大家共同学习---江小白。

现状

近些年，各种新的零知识证明算法层出不出，各有各的特点，各有各的优势。借用V神系列文章里的一张图来简单呈现下当前的零知识证明算法现状。

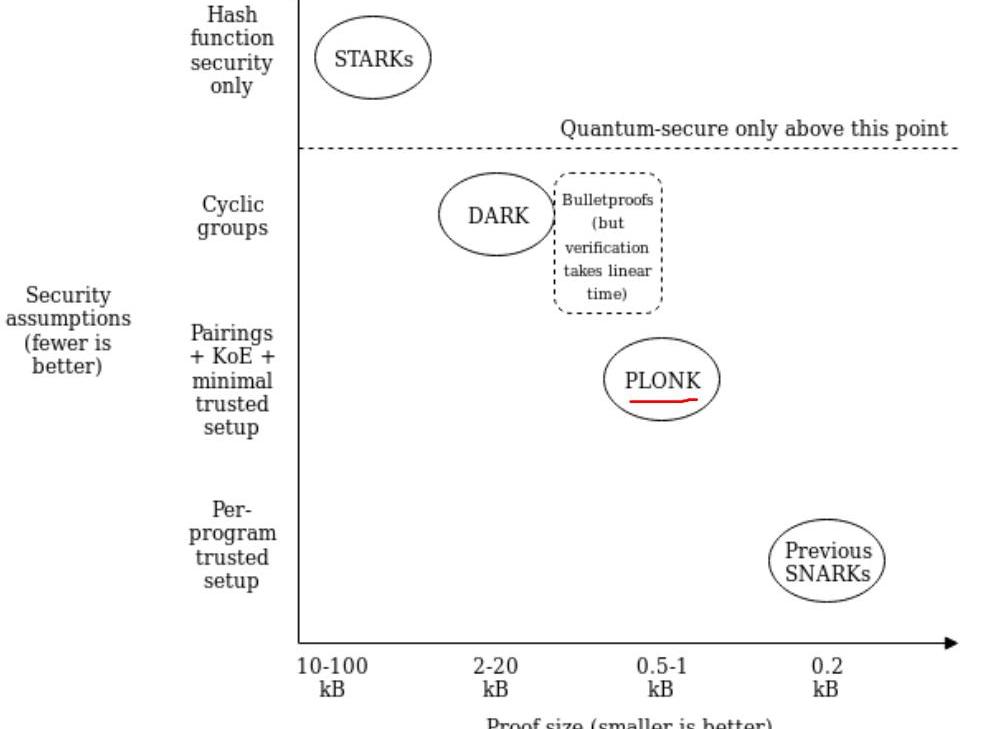
从图中可以简单总结出以下几点：

理论上安全性最高的是STARKs算法，不依赖数学难题假设，具有抗量子性；Proof大小上最小的是SNARKs算法，如Groth16;PLONK算法在安全性上和Proof大小上，位于上述两者之间；其他的这里不做过多阐述，如想了解零知识证明更多信息，可参考链接；对于SNARKs算法，绕不开的一个点就是中心化的TrustSetup，也称之为CRS(theCommonReferenceString)。而无论是PGHR13,Groth16,还是GM17算法，它们的CRS都是一次性的，不可更新的。即，不同的问题将对应着不同的CRS，这在某些场景下，会变得比较麻烦。这些存在的问题，变成了PLONK，SONIC这类算法的一个优势，它们算法虽然也需要中心化的可信设置，但是它的CRS具有一定的普适性。即，只要电路的大小不超过CRS的上限阈值，一些证明问题就可以共用一个CRS，这种CRS称之为SRS(universalStructuredReferenceString)，关于SRS的定义，详细的可参考SONIC协议里的第3小节。PLONK算法继用了SONIC算法的SRS的思想，但是在证明的效率上，做了很大的提升。接下来，让我们详细的介绍下PLONK算法的具体细节，主要从下面四个小节去分享：

萨尔瓦多总统：比特币进程会经历一条学习曲线，萨尔瓦多有权迈向第一世界:9月7日消息，萨尔瓦多比特币法案即将生效之际，萨尔瓦多总统Nayib Bukele再次发推称：和所有创新一样，比特币进程会经历一条学习曲线。未来的每一条路都是这样，不是能一蹴而就的。但我们必须打破过去的范式，萨尔瓦多有权迈向第一世界。之前报道，Bukele称该国已买入400枚比特币。[2021/9/7 23:05:38]

电路的设计--描述PLONK算法的电路的描述思想；置换论证或者置换校验--复制约束，证明电路中门之间的一致性；多项式承诺--高效的证明多项式等式的成立；PLONK协议--PLONK协议剖析；电路

PLONK算法电路的描述和SONIC算法一直，具体的过程可以参考李星大牛的分享，已经写的比较详细且易懂。在这个小篇幅里，我想主要分享下我自己的两点想法：

无论是什么样的电路描述方式，电路的满足性问题都要归结于2点，门的约束关系和门之间的约束关系成立；在SNARKs系列的算法里，电路的描述单元都是以电路中有效的线为基本单元，具体的原理可以参考我之前分享的文章，而在PLONK，SONIC以及HALO算法里，电路的描述单元都是以门为基本单元。这两种电路的不同描述方式带来了一定的思考。那就是，之前在研究SNARKs算法时，我们都已经相信一个事实，“多项式等式成立，就代表着每个门的约束成立”，然后推断，整个电路逻辑都是成立；在这个过程中，并没有额外的去证明门之间的一致性成立；但是在PLONK算法里，除了要证明多项式等式成立外，还要额外的用置换论证的数学方法去证明门之间的约束关系，即复制约束。为何会有这样的区别？希望有心的读者能一起在评论区探讨这个问题？我个人理解是因为电路的描述方式的不同：

声音 | 江苏省政协委员：希望以区块链技术为核心建设学习型社区:金色财经报道，1月15日下午，江苏省政协委员、光华教育集团董事长、盐城外国语学校董事长鲁育宗表示，我们希望通过有效整合资源，以区块链技术为核心，充分利用现有高等院校、职业院校、社会学习中心等各类型学校和企业、社会资源，建设一个集在线教育、学分银行以及数据与人才中心等功能于一体的学习型社区，以学生为中心建设新的专业人才培养和供应体系，打造人才培养共同体，为社会培养更多更好的人才，为建设‘学习型社会’作出新的贡献。[2020/1/16]

PLONK算法里，电路描述的单元是门，它为每个门定义了自己的L,R,O，因此需要证明门之间的一致性；SNARKs算法里，电路描述的单元是线，门与门之间的值用的是同一个witness，因此不用额外证明一致性；置换论证

前面我们说过，在PLONK算法里，需要去证明门之间的约束关系成立。在做具体的原理解释之前，我们先简单的过一下PLONK协议的过程，如下图所示：

可描述为：

根据电路生成三个多项式，分别代表这电路的左输入，右输入，输出；利用置换校验协议，去证明复制约束关系成立；步骤3和4，校验门的约束关系成立。其中第1点已经在电路小节里阐述过了，接下来，将详细的讲解多项式置换校验的原理。先从简单的场景去讲解：

声音 | 光明日报：利用区块链开展分布式学习记录 建立学生个人学习成长档案:《光明日报》今日发表题为“以新思维新技术破解教育评价痛点”的评论文章。文中表示，随着人工智能、大数据、区块链等新一代信息技术的发展，新技术正在触发一场教育评价方式的深刻变革。未来，在新技术的支持下，教育评价将从散点式的成绩记录转向全景式的数据采集，利用区块链技术开展分布式学习记录，建立学生的个人学习成长档案，认证学生的多样化学习成就，重点考察学生的非认知能力发展，有效防止数据丢失或被恶意篡改，助力解决学生综合素质评价中存在的信任问题。[2019/12/10]

单个多项式的置换校验

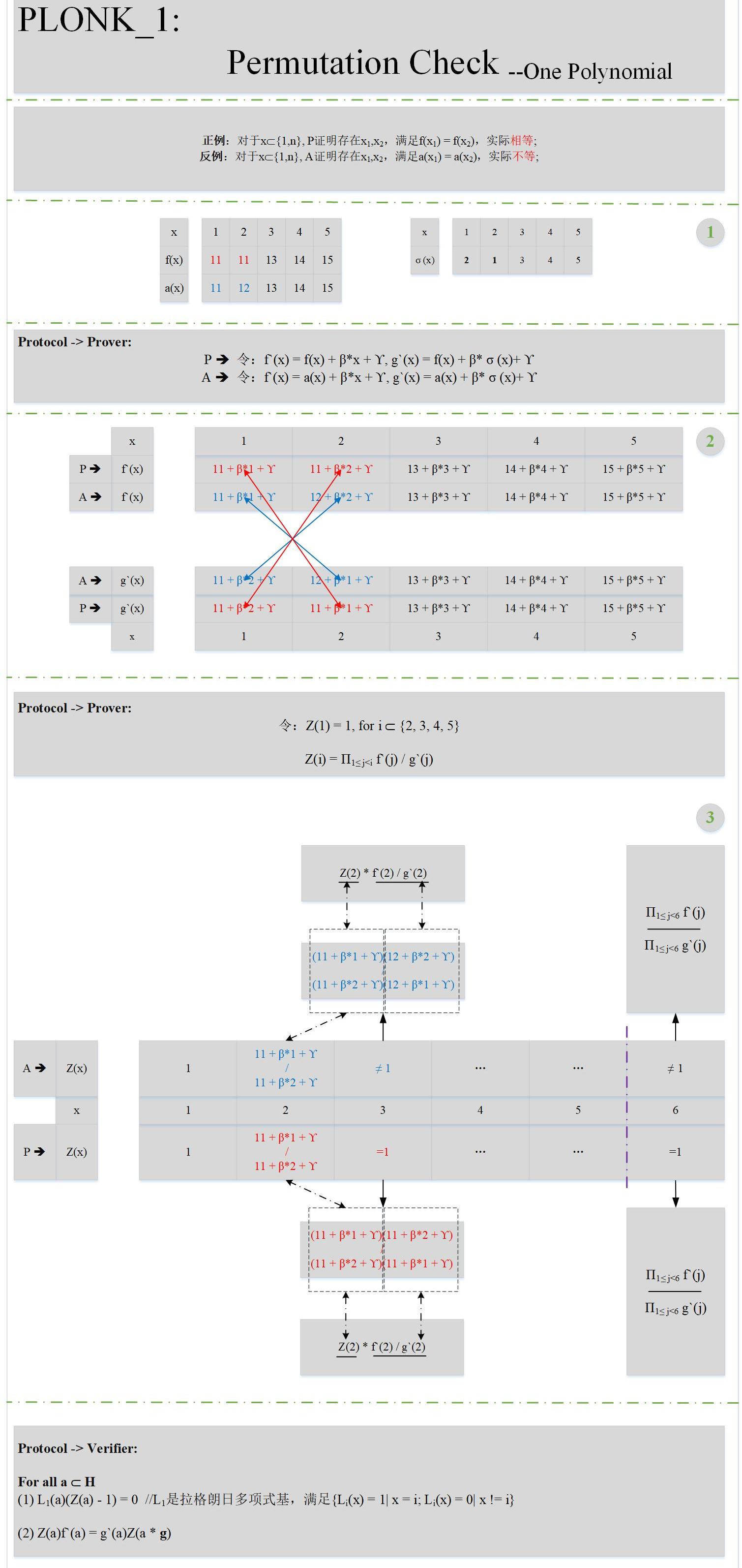
其实就是证明对于某个多项式f，存在不同的两个点x,y，满足f(x)=f(y)。下面来看具体的原理：

金色相对论 | 肖臻：区块链核心技术还是属于分布式系统、密码学等计算机传统领域，跟机器学习也有很好的结合点:在今日的金色相对论中，针对“区块链、分布式系统以及机器学习领域的研究具体应用有哪些”的问题，北京大学计算机系研究员、博士生导师，肖臻表示，虽然区块链表面上是个新的领域，其实核心技术还是属于分布式系统、密码学等计算机传统领域，跟机器学习也有很好的结合点，目前我们正在致力于利用该技术实现智能合约的高效、细粒度并发执行。已有的区块链技术（比如以太坊中的智能合约）只支持单线程，就是因为在多核环境下并行程序的执行存在不确定性，影响区块链中的节点达成共识。我的课题组开发的确定性重演技术有希望极大地提高智能合约的执行效率，成为区块链3.0中的核心技术。我们的另一项成果是基于多智能体的智能决策系统，通过强化学习技术使得各智能体在去中心化的情况下独立做出判断，实现某个预先设定好的效益函数的最大化。[2019/9/12]

上图中加入了一个正例P，一个反例A，方便大家理解置换校验的原理。有几点需要解释的是：

而经过仔细剖析Z的形式，不难发现，Z(n+1)其实就是两个函数所有值的乘积的比值(不知是否等同于V神文章里的坐标累加器？)。理论上是等于1。因此，我们需要设计这样的一个多项式Z，需满足：deg(Z)<n

声音 | Circle CEO评论Facebook收到议员联名信：Maxine Waters需要倾听并学习:Circle首席执行官Jeremy Allaire就“美国众议院民主党议员联合致信Facebook，呼吁其暂停Libra开发”一事评论表示：我想告诉Maxine Waters（众议院金融服务委员会主席），你需要倾听并学习，因为（加密）技术正在以惊人的速度发展。这不仅仅是一个处于早期阶段的实验项目，也不仅仅是Facebook上的一个空白页面。在全球范围内，成千上万的工程师在不断地建造东西——这是无法停止的，它在增长，且还在继续增长。我想说的是，现在是决策者去学习的时候了，因为这是全球经济的一个重大突破。 此前报道，包括Maxine Waters在内的美国众议院民主党议员周二向Facebook发布公开信，呼吁其暂停所有的Libra开发。[2019/7/5]

Z(n+1)=1

2.乘法循环群刚好可以满足这个条件，如果设计一个阶为n的一个乘法循环群H，根据群的性质可以知道Z(g)=Z(g^(n+1))。因此，在设计Z时，会保证Z(g)=1；上图中的自变量的取值也将从{1...n}变成{g...g^n}。所以在上图中验证的部分，a其实已经换成了群H里的所有元素。

3.根据论文中的协议，多项式Z是会发给可信第三方I验证方V会从I处获取到多项式Z在所有a处的取值，然后依次校验。

下面具体看一下论文中的定义：

从定义中可以看出：多项式f,g在范围内具有相同的值的集合；下面看一下论文中具体的协议部分，结合上述解释的3点：

说明：图4中的f,g对应图3中的f。即f,g是同一个多项式。其实只要是相同的值的集合，也可以不用于是同一个多项式。图3是一个特例而已。

跨多项式的校验

其实就是证明对于某个多项式f，g，存在两个点x,y，满足f(x)=g(y)。与存在两处不同：

多个多项式；不强制x,y的关系，即也可以等，也可以不等；有了(1)小节的基础，这次我们先看一下相关的定义：

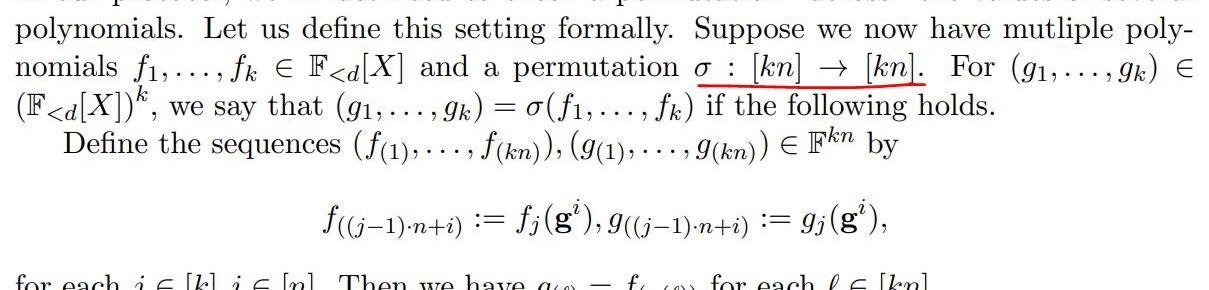
从定义可以看到，这次是两个多项式集合见的置换校验算法。从标注的部分可以看出：

两个多项式集合仍然具有相同的值的结合；为了区分集合里的多项式，自变量的索引得区分开来；因此，可以想象的到，如果存在两个多项式f,g，想要证明f(x)=g(y)，那么根据以上描述可以判断{f1,f2}={f,g}={g1,g2}。也保证了上述第1点的成立。

下面我们看一下具体的原理：

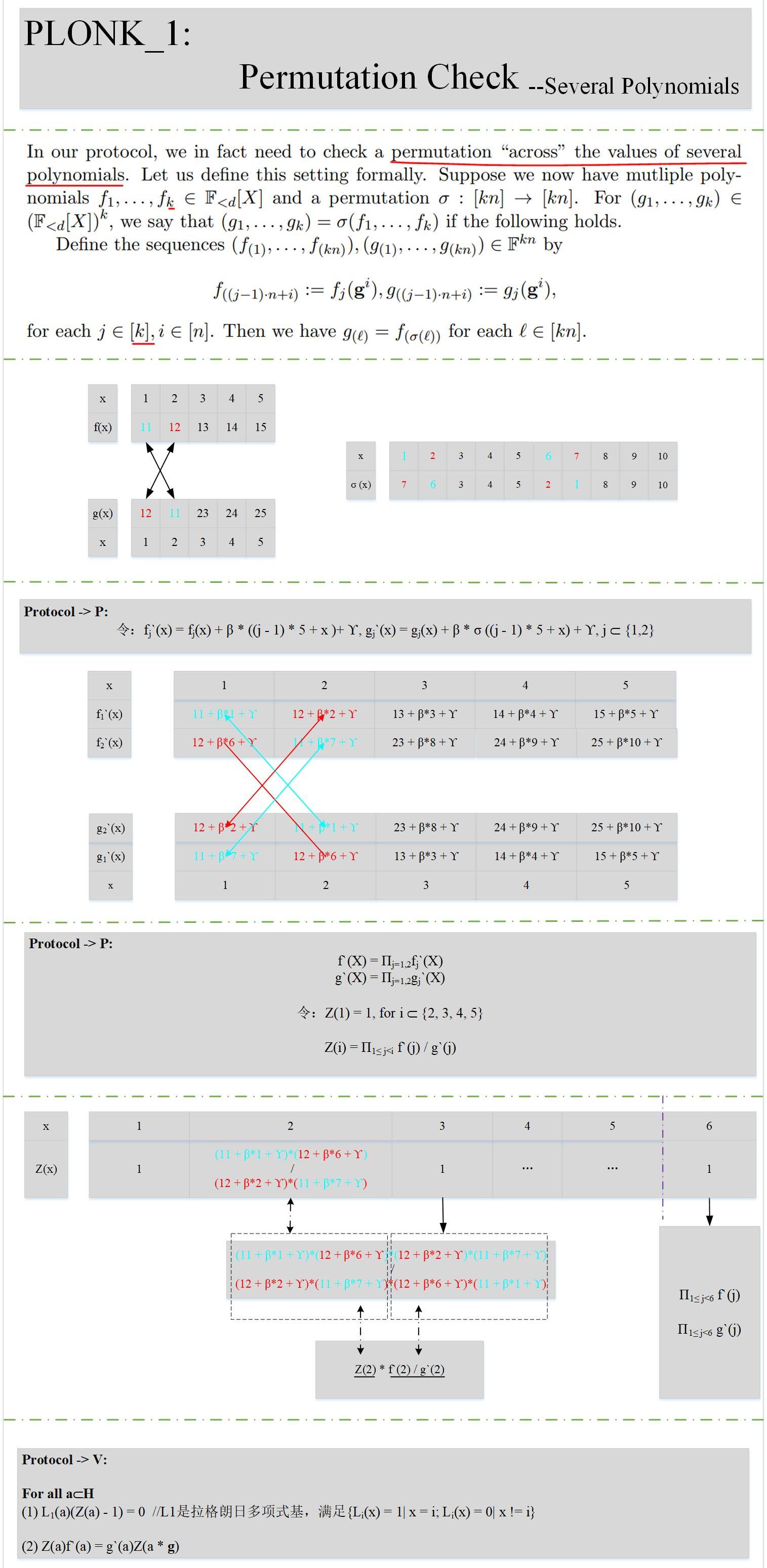
和(1)小节相比，证明方P增加了些工作量，验证方V工作量不变。结合上述描述，也能很容易的理解其数学原理。

说明：至此，其实我们已经慢慢的接触到PLONK算法的核心了，前面我们讲到，电路的满足性问题除了门的约束关系还有门之间的约束关系。

比如一个输入x，它既是一个乘法门的左输入，又是另外一个乘法门的右输入，这就需要去证明L(m)=R(n)，这就是跨多项式的置换校验。

下面再给出论文里的协议内容：

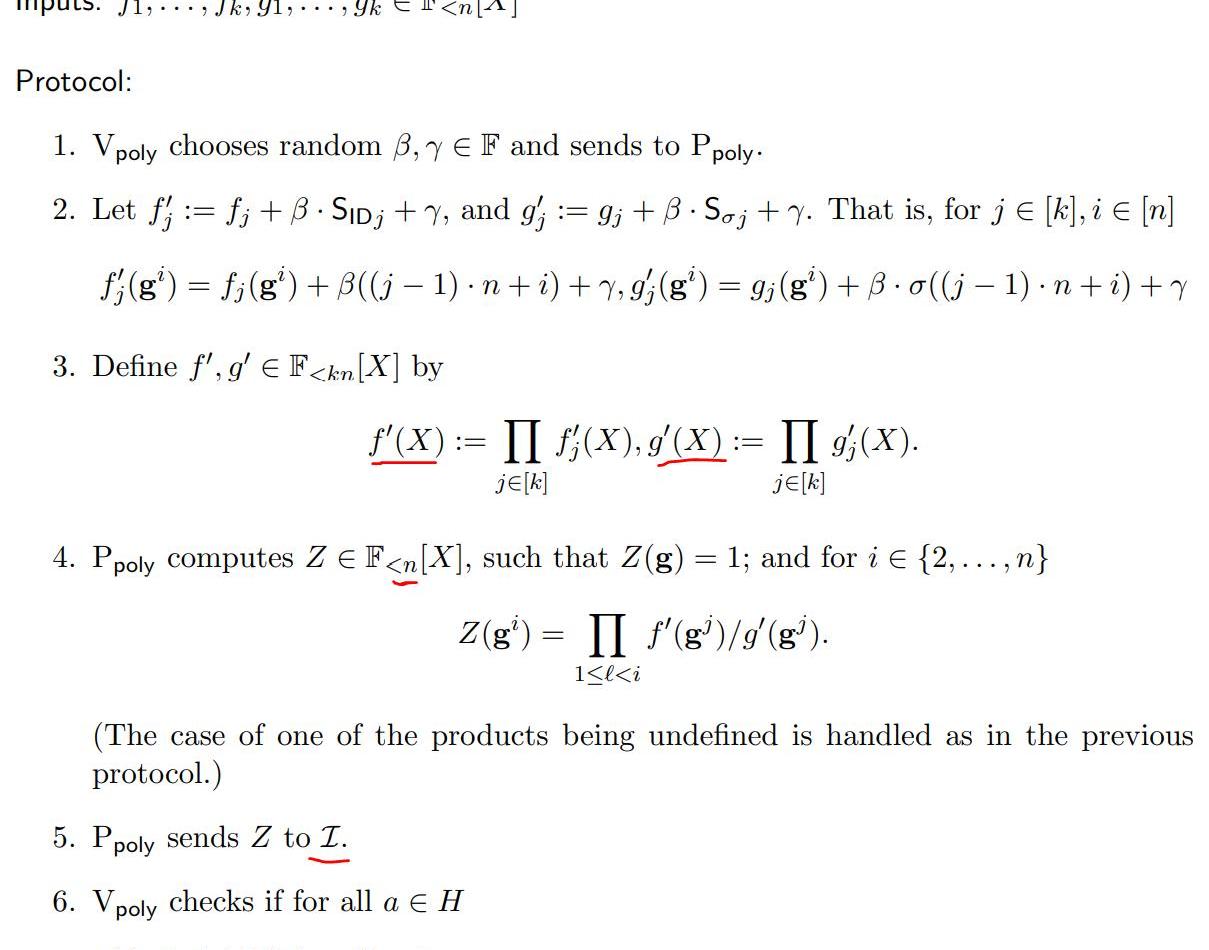
至此，本篇文章已经描述了，在PLONK算法里，电路的设计以及复制约束的成立验证两大部分，接下来，将会另起一片文章，去分享门约束的成立和整个协议的具体步骤。

以上都是作者小白的个人理解，还希望各位读者多多指教，谢谢。

标签：LONPLO区块链CRSpoloniex交易所可靠吗UPLOAD币区块链的未来发展前景怎么样CRS价格

火币交易所热门资讯